Analisis Soal Pembentukan Bayangan Pada Gabungan Dua Lensa Cembung Tipis

AhmadDahlan.NET – Pembentukan bayangan di depan sebuah lensa tipis bisa dilakukan dengan analisis geometri, lantas bagaimana jika benda tersebut terletak di depan lensa ganda.Sifat pembentukan bayangan pada lensa tunggal ataupun ganda tetap terbentuk berdasarkan hukum snelius tentang pembiasan dengan demikian analisa-nya bisa dilakukan dengan pendekatan Geometri.

Untuk memudahkan analisa mari kita buat kasus gabungan dua lensa tipis.

Contoh Soal :

Sebuah benda diletakkan 60 cm di depan dua buah lensa konvergen. Jika focal point dari lensa masing-masing f₁ = 20 cm dan f₂ = 25 cm dan terpisah sejauh 60 cm, maka tentukan jarak dan perbesaran bayangan-nya!

Solusi

Untuk menyelesaikan kasus ini, kita analisis konsep pembentukan bayangan yang terjadi di masing-masing lensa. Kta mulai dari lensa pertama dengan menggunakan sinar istimewa.

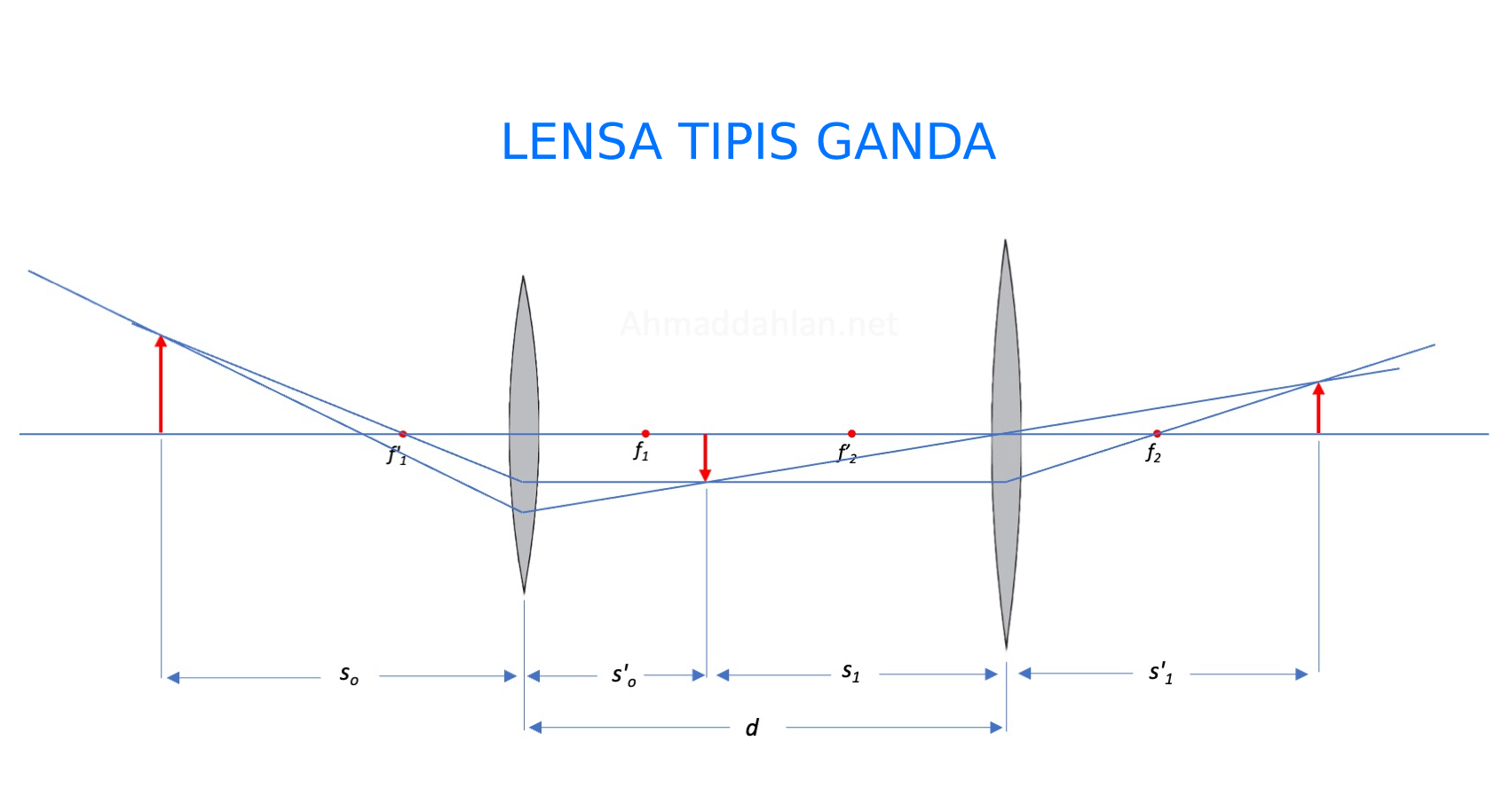
Pelukisan bayangan dilakukan dengan dua sinar istimewa dengan keterangan sebagai berikut :

f₁ = jarak focal point lensa pertama (20 cm)
s_o = Jarak Benda ke lensa (60 cm)
s’_o = Jarak bayangan benda di lensa pertama

jarak s’_o bisa dihitung dengan persamaan pembentukan bayangan dilensa tipis :

\frac{1}{f_1}=\frac{1}{s_o}+\frac{1}{s'_o}

\frac{1}{s'_o}=\frac{1}{20}-\frac{1}{60}=\frac{3-1}{60}=\frac{1}{30}

dengan jarak bayangan adalah s’_o = 30 cm.

Perbesaran bayangan pada lensa pertama adalah :

m =- \frac{s'_o}{s_o}=-\frac{30}{60}=-0,5

Dengan demikian sifat bayangan yang terbentuk di lensa pertama adalah :

1. diperkecil
2. terbalik
3. nyata

Lensa II

Perhatikan jarak 30 cm ini menjadi jarak benda di belakang lensa pertama. Karena jarak antar lensa terpisah sejauh d=80 cm sehingga bayangan pertama ini akan menjadi benda di lensa kedua. Jarak ini dari lensa II kita sebut saja s₁ dengan jarak :

d= s'_o + s_1 

80 cm = 30 cm +s'_1

s’₁ = 50 cm.

Selanjutnya kita lukis pembentukan byangan pada lensa ke dua.

Pembentukan bayangan pada lensa ke dua adalah

\frac{1}{f_2}=\frac{1}{s_1}+\frac{1}{s'_1}

\frac{1}{s'_1}=\frac{1}{50}-\frac{1}{25}=\frac{2-1}{50}=\frac{1}{50}

maka bayangan terbentuk di belakang lensa dengan s’₁ = 50 cm.

Perbesaran bayangan nya adalah :

m = -\frac{s'_o}{s_o}=-\frac{50}{50}=-1

Dengan demikian sifat bayangan akhir adalah :

1. Sama besar dengan bayangan pertama atau diperkercil dari ukuran objek
2. tegak lurus
3. nyata

Perbesaran bayangan total dapat dihitung secara langsung dengan

m_{total}=m_1.m_2=(-0.5)(-1.0)=0.5

Hasilnya adalah positif 0.5 dengan demikian bayangan pasti tegak lurus.

Persamaan tanpa angka :