AhmadDahlan.NET – Ketika kita melempar sebuah batu ke arah depan seperti saat melembar buah mangga, gerak batu tersebut akan membentuk lintasan melengkung seperti parabola. Demikian saat sebuah boleh ditendang, lintasan yang terbentuk adalah gerak parabola, hanya saja karena massa jenis bola relatif rendah, maka hambatan udara terkadang akan merubah arah gerak bola dari lintasan parabola sempurna.
Daftar Isi
Gerak parabola juga kadang disebut gerak peluru jika meurujuk pada artikel berbahasa inggris yang menyebut gerak parabola sebagai Projectile Motion. Gerak ini adalah gerak vektor yang bisa dianalisis dengan solusi matematis.
A. Gerak Parabola
Gerak parabola dapat didefenisikan ketika sebuah benda dilemparkan dengan kecepatan awal v0 pada sudut θ yang diukur dari garis horisontal. Benda ini akan bergerak dengan dua vektor kecepatan yakni ke arah vertikal (y) dan gerak ke arah horisontal (x).
Segera setelah kecepatan arah y menjadi nol, benda akan mencapai ketinggian maksimal (hmaks). Titik ini menjadi titik balik ke arah sumbu y, sampai akhirnya benda mencapai tanah. Setelah mencapai tanah jarak ini disebut sebagai xmaks. xmaks ini kadang disebut sebagai jangkaun maksimum dan disimbolkan R dari kata range.

B. Persamaan Gerak Parabola tanpa Hambatan Udara
Analisis gerak parabola dilakukan dengan pemodelan tanpa hambatan udara sehingga seluruh gerak hanya dipengaruhi oleh tiga variable yakni kecepatan awal (v0), percepatan gravitasi (g) dan ketinggian awal (h0). Analisis dipisahkan ke dalam sumbu kartesian x dan y karena gerak parabola sederhana adalah gerak dua dimensi.

Sehingga vektor geraknya adalah :
x(0) = 0
x’(0) = v0 cos θ
y(0) = 0
y’(0) = v0 sin θ
Jika hambatan udara diabaikan maka gerak arah sumbu x adalah gerak lurus beratuan (GLB) dan gerak ke arah sumbu y adalah gerak yang dipengaruhi oleh percepatan grafitasi (g). Pada saat bergerak ke atas maka geraknya diperlambat dan ketika ke bawah dipercepat.
Dengan demikian kita dapat selesaikan masalah gerak parabola dengan metode diferensial untuk du akomponen gerak yakni :
Komponen x
x”(t) = 0
x’(t) = v0 cos θ
x(t) = v0t cos θ
Komponen y
y”(t) = -g
y’(t) = -gt + v0 sin θ
y(t) = -1/2 gt + v0t sin θ + c
c adalah kontantan yang menunjukkan ketinggian awal dari benda jika ketinggian awalnya 0 maka persamaan nya menjadi y(t) = -1/2 gt + v0t sin θ.
Persamaan ini sudah bisa menggambarkan gerak parabola sebagai fungsi dari t, namun tidak untuk mengetahui jangkaun maksimum dari gerak benda karena arah g berubah setelah vy menjadi 0. Kedua persamaan ini bisa disubtitusikan untuk menformulasikan persamaan gerak horisontal x dengan memasukkan nilai t
t = \frac{x}{v_0 \cos θ}setelah masukkan nilai t ke persamaan sumbu y sehingga kita bisa dapatkan persamaan y sebagai fungsi dari x dengan demikian :
y_{x}=h +v_0\sin θ\left ( \frac{x}{v_0 \cos θ}\right )-\frac{1}{2}g \left ( \frac{x}{v_0 \cos θ}\right )^2persamaan ini bisa disederhanakan
y_{x}=h +x \tanθ -\frac{1}{2}\frac{gx^2}{v_0^2}\sec^2θPersamaan ini adalah persamaan umum y sebagai fungsi dari x.

Karena yx ini tidak melulu sejajak dengan sumbu maka kita sebuy persamaan persamaan posisi yakni px.
1. Persamaan Jangkauan Maksimum
Dalam gerak para bola biasanya timbul pertanyaan tentang jangkauan maksimum dari gerak parabola. Misalkan setiap θ ini berubah akan berdampak pada perubahan jarak yang ditempuh kita misalkan saja xi. Selain θ sebenarnya jaangkauan gerak parabola ditentukan dengan kecepatan awal v0, tapi dalam pemodelan ini kita tinjau v0 tetap.

Karena setiap x akan berubah setiap berubah θ, maka x ini adalah fungsi dari dθ, dengan demikian kita sebuat saja fungsi yx digunakan untuk menemukan persamaan umum gerak ke arah horisontal. Kita sebuah saja persamaan ini adalah ψ. Dengan demikin persamaan yx bisa ditulis sebagai berikut :
ψ'=y'=h +d_θ\tanθ -d_θ^2\frac{1}{2}\frac{g}{v_0^2}\sec^2θmaka :
ψ'.d'_θ=d_θ\sec^2θ+d'_θ\tan θ-\frac{g}{v^2}d_θ^2\secθ(\sec θ\tanθ)+d_θd'_θ\sec^2θkarena
d'_{θ_m}=0maka
0=d'_{θ_m} \sec^2θ-\frac{g}{v^2}d^2_{θ_m} \secθ_m \tan θ_md_{θ_m}=\frac{v^2}{g}\cotθ_m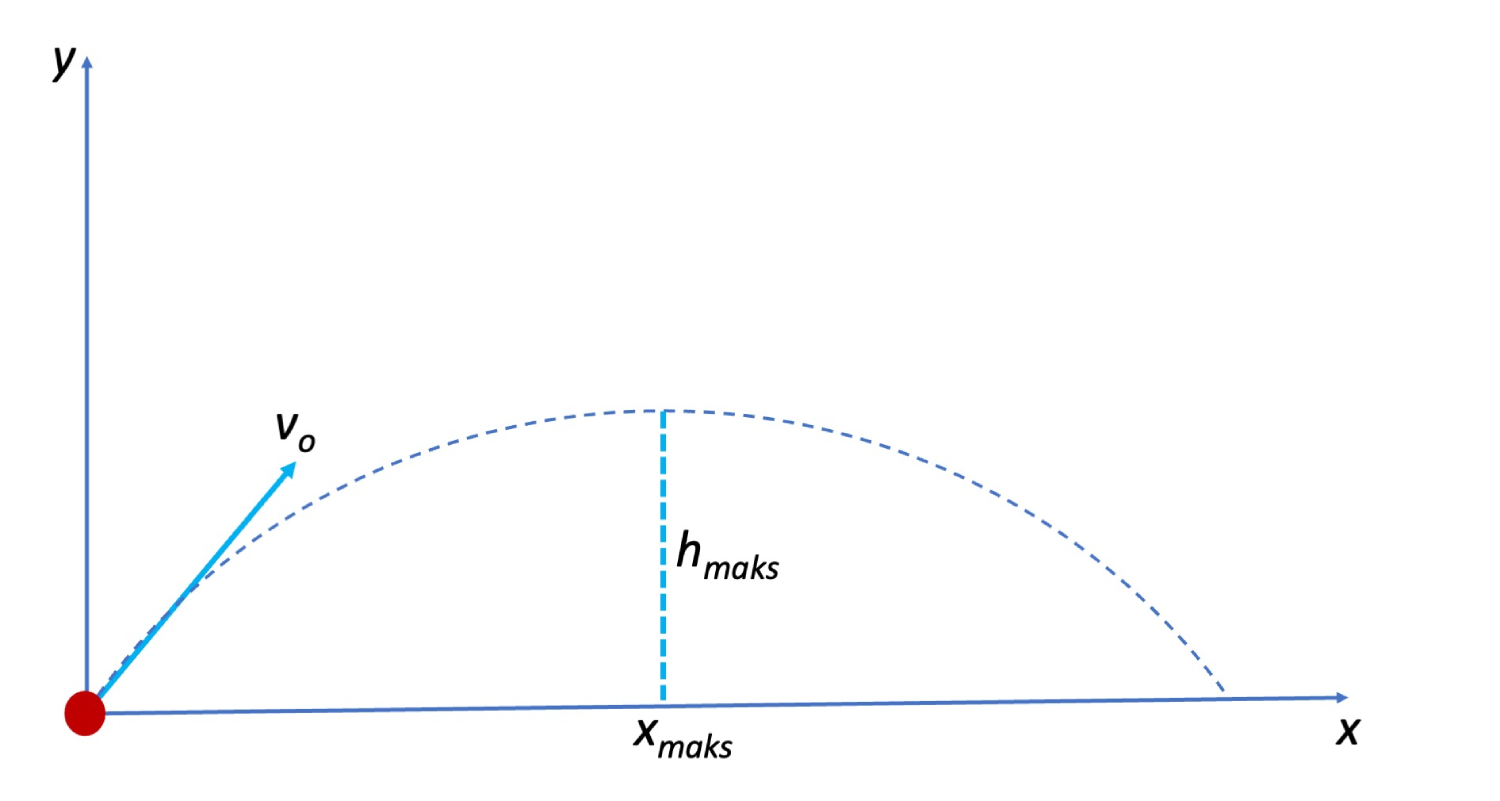
Leave a Reply
You must be logged in to post a comment.