Contoh Kasus Analisis Data Statistik Deskriptif Berkelompok dengan Tabel Distribusi Frekuensi

Analisis data statistik deskriptif berkelompok dengan tabel distribusi frekuensi digunakan untuk menganalisis data yang belum memiliki standar penilaian yang jelas. Hal ini disebabkan belum adanya standar-standar yang baku terkait nilai-nilai yang melekat pada kelompok data yang sedang di ukur. Hal ini menyebakan tidak ada standar baku konversi skor menjadi nilai.

Daftar Isi

Contoh Kasus Analisis Data Statistik Deskriptif

Mari kita misalkan sebuah hasil pengukuran sebuah variabel untuk 40 subjek menghasilkan data sebagai berikut :

31	33	78	79	45	50	59	45
34	76	57	63	52	77	75	73
27	34	55	53	82	82	60	63
55	56	42	44	67	69	87	47
43	23	52	66	80	43	48	84

Analisis statistik deskriptif data berkelompok dilakukan dengan langkah berikut :

Mengurutkan Data
Menentukan Rentang Data
Menentukan Jumlah kelas
Menghitung Interval Kelas
Menyusun Kelas
Menentukan Distribusi Frekuensi
Menghitung Rata-Rata
Menghitung Variansi dan Standar Deviasi

A. Mengurutkan Data

Langkah pertama dilakukan dengan mengurutkan data. Bisa dilakukan dari data terkecil ke data terbesar. Bagian ini bukanlah langkah esensial namun sangat membantu dalam menghitung jumlah frenkuensi berdasarkan interval kelas.

Adapun urutan tersebut adalah :

23	27	31	33	34	34	42	43
43	44	45	45	47	48	50	52
52	53	55	55	56	57	59	60
63	63	66	67	69	73	75	76
77	78	79	80	82	82	84	87

B. Menghitung Rentang Data

Rentang data adalah interval data dari tertinggi sampai ke terendah. Rentang ini dhitung dengan rumus

R = n_{max}-n_{min}

Dimana :

n_max : skor maksimum
n_min : skor minimum

Berdasarkan tabel data yang sudah diurutkan didapatkan

n_max : 87
n_min : 23

Rentang kelas adalah

B. Menentukan Jumlah Kelas

Jumlah kelas adalah banyak kelas yang akan dibuat. Biasanya Kelas ini dibuat untuk membuat kategori-kategori berdasarkan kelompok data.

Secara umum jumlah kategori yang banyak digunakan adalah ganjil mulai dari 3, 5, 7, dst. Jumlah kelas ini dapat ditentukan sesuai dengan keinginan.

Ada juga pendapat yang menyatkan jumlah kelas dapat dihitung dengan rumus strugress yakni

k=1+3,3 \log n

keterengan

k : jumlah kelas
n : banyaknya data.

Kalau menggunakna rumus Trugess maka jumlah data 40 memiliki panjang kelas

k = 1 + 3,3 (\log 40) = 6,28

Jadi jumlah kelas yang dipakai adalah 6. Jika anda ingin menggunakan 5 kelas juga bisa. Hal ini bergantung kebutuhan.

C. Menentukan Interval Kelas

Interval kelas adalah jarak antara batas kelas bawah dan batas kelas atas. Interval ini digunakan untuk (1) membagi data ke dalam beberapa kelompok kelas dan (2) dasar menentukan berapa banyak jumlah data dalam interval kelas tersebut

i = \frac{R}{k}=\frac{n_{max}-n_{min}}{k}

dengan demikian interval kelas ini adalah

i=\frac{87-23}{6} = 10.66

Interval kelas ini adalah bilangan bulat sehingga intervalnya bisa dibulatkan ke atas atau ke bawah. Bisa dipilih 10 atau 11. Hal ini bergantung dari rentang data, namun pada umumnya dibulatkan ke atas agar distribusi interval kelas terpenuhi secara keseluruh.

Catatan

Misalnya kita mengambil 10, maka jumlah data yang terpenuhi rentangnya sepanjang 60 padahal rentang data sendiri 87-23 = 65. Hal ini membuat tidak semua data bisa masuk dalam tabel. Contoh, ketika kita batas kelas bawah diambil 23 maka batas kelas atas hanya sampai 83, padahal ada data pada angka 87.

Jika interval kelas yang digunakan 11 maka batas. Maka rentang kelasnya adalah 66. Hal ini membuat seluruh rentang kelas dapat terpenuhi. Perhatikan retang dadat adalah 65 sedangkan rentang data yang disusn berdasarkan kelas 66 dengan demikian rentang kelas lebih panjang daripada retnang data. Hal ini bukanlah masalah karen kita bisa menggeser batas bawah kelas yakni 23 ke 22 atau batas atas dari 87 ke 88.

D. Menyusun Kelas

Menyusun data kelas dilakukan dengan membuat tabel dengan jumlah bari sejumlah dengan rentang kelas. Panjang kelas dapat dimulai dari batas bawah kemudian ditambah rentang kelas (11) dikurang 1.

Yah bisa, bahkan bisa dimulai dari 21, asalah seluruh data tercakup. Dalam kasus data di atas, kita tidak bisa memulai dari 21 karena batas atas akan turun menjadi 86 padahal ada data yang bernilai 87.

Mengapa dikurang 1? Karena batas bawah adalah anggota dari kelas itu sendiri. Misalkan kita ambil 22 sebagai batas bawah, maka kelasnya sebagai berikut

No	Kelas
1	22 – 32
2	33 – 43
3	44 – 54
4	55 – 65
5	66 – 76
6	77 – 87

Apakah bisa di mulai dari 23?

Demikian pula sebaliknya kita tidak bisa memulai dari 24, karena ada aggota data yang tidak masuk yakni 23.

E. Menentukan Frekuensi Kelas

Frekuensi kelas adalah jumlah data yang masuk dalam interval kelas tertentu. Frekuensi kelas adalah konsep utama dari tabel distribusi frekuensi karena hal ini menjadi deskripsi dari perilaku data itu sendiri.

Sekarang kita distribusikan data yang sudah dirutukan di awal.

23	27	31	33	34	34	42	43
43	44	45	45	47	48	50	52
52	53	55	55	56	57	59	60
63	63	66	67	69	73	75	76
77	78	79	80	82	82	84	87

Dari tabel di atas, dapat diketahui jika kelas 22 – 32 terdiri dari 3 anggota yakni 23, 27, dan 31. Lakukan hal yang sama untuk kelompok kelas lain.

No	Kelas	f_i
1	22 – 32	3
2	33 – 43	6
3	44 – 54	9
4	55 – 65	8
5	66 – 76	6
6	77 – 87	8
	Jumlah	40

Sampai disini kita sudah mendapatkan jumlah distribusi frekuensi berdasarkan tabel distribusi frekuensi yang telah dibuat. Misalnya kita membuat kategori sebagai berikut

77 – 87 : Sangat Baik Sekali
66 – 76 : Sangat Baik
55 – 65 : Baik
44 – 54 : Cukup
33 – 43 : Kurang
22 – 32 : Sangat kurang

Penentuan kategori dibutuhkan konstruksi dan teori tambahan sesuai dengan variable yang diukur. Misal untuk penilaian mata kuliah

77 – 87 : A
66 – 76 : B
55 – 65 : C
44 – 54 : D
33 – 43 : E
22 – 32 : F

F. Menentukan Rata-Rata Data Berkelompok

Rata-rata data berkelompok dapat dihitung dengan persamaan

\bar x=\frac{\Sigma x_if_i}{n}

keterangan

x_i : nilai tengah kelas i
f_i : jumlah frekuensi kelas i
n : jumlah data

nilai tengah kelas i (x_i) dapat dhitung dengan persamaan

x_i=batas \ kelas \ bawah\ i + \frac{batas\ kelas \ atas \ i - batas\ kelas \ bawah \ i }{2}

misalnya kelas 22 – 32, nilai x_i adalah

x_i=22+\frac{32-22}{2} =27

Berdasarkan ini kita dapat tabel distribusi berupa

No	Kelas	f_i	x_i	f_i .x_i
1	22 – 32	3	27	81
2	33 – 43	6	38	228
3	44 – 54	9	49	441
4	55 – 65	8	60	480
5	66 – 76	6	71	426
6	77 – 87	8	82	656
	Jumlah	40	–	2.312

Berdasarkan data dari tabel diatas dapat dihitung rata-rata data berkelompok sebesar

\bar x=\frac{\Sigma x_if_i}{n} = \frac{2.312}{40}=57,8

nilai rata-rata data berkelompok sebesar 57,8.

G. Variansi dan Standar Deviasi Data Berkelompok

Variansi dihitung dengan persamaan :

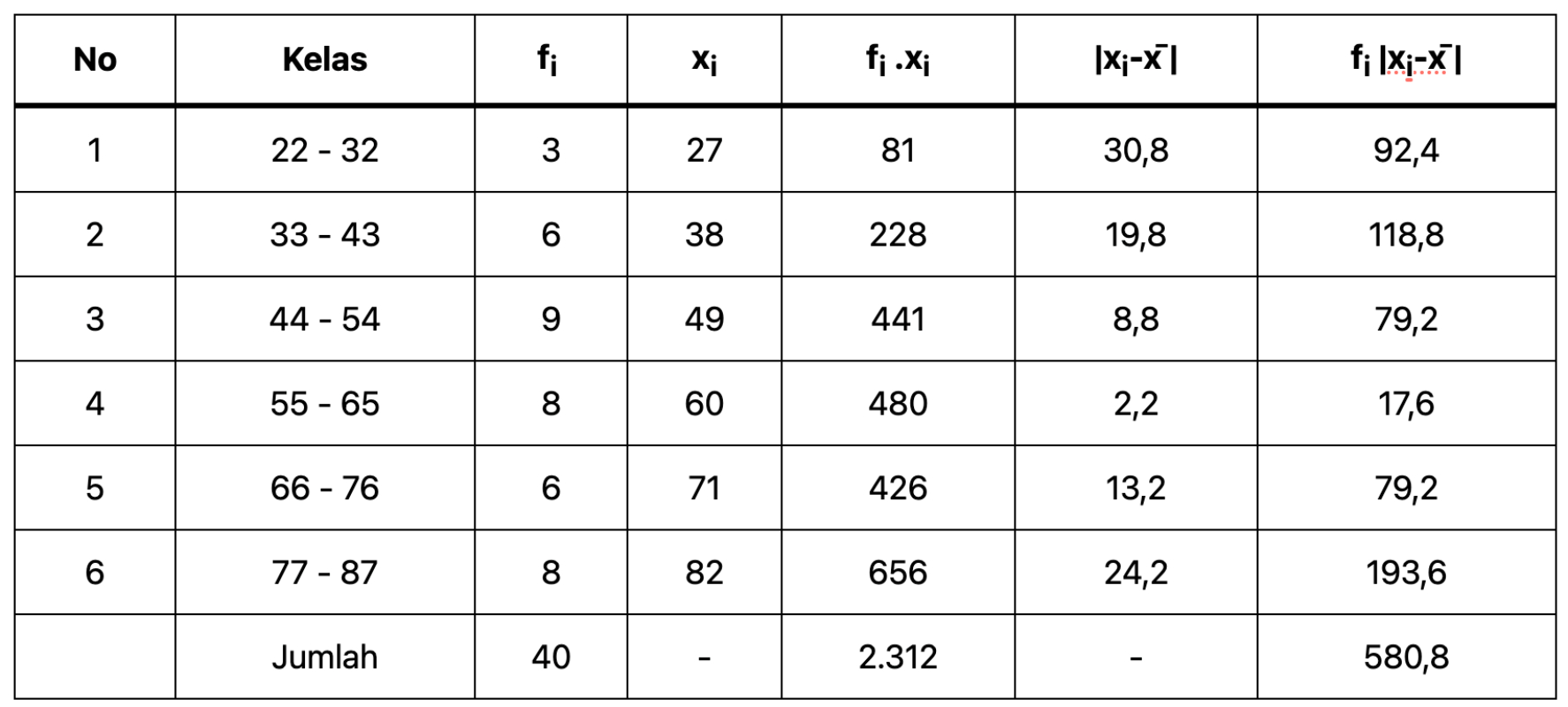
S^2=\frac{\Sigma f_i|x_i-\bar x|}{n}

No	Kelas	f_i	x_i	f_i .x_i	\|x_i-x̄ \|	f_i \|x_i-x̄ \|
1	22 – 32	3	27	81	30,8	92,4
2	33 – 43	6	38	228	19,8	118,8
3	44 – 54	9	49	441	8,8	79,2
4	55 – 65	8	60	480	2,2	17,6
5	66 – 76	6	71	426	13,2	79,2
6	77 – 87	8	82	656	24,2	193,6
	Jumlah	40	–	2.312	–	580,8

Dengan demikian Variansi data berkelompok ini adalah :

S^2=\frac{580,8}{40}=14,52

Standar deviasi adalah :

S=\sqrt{14,52} =3,81

Dengan demikian rata-rata data berkelompok di atas secara lengkap dapat ditulis

\bar x = 57,80 ± 3,81

H. Tabel Laporan Hasil Statistik Distribusi Frekuensi

No	Nama Variabel	Skor
1	Jumlah Data	40
2	Skor Maksimum	87
3	Skor Minimum	23
5	Rata-rata	57,80
6	Standar Deviasi	3,81