Gerak Parabola adalah gerak perpaduan antara geral lurus beraturan pada sumbu x dan gerak berubah beraturan pada sumbu y. Gerak ini memiliki lintasan seperti parabola terbalik sehingga disebut sebagai gerak parabola.
Daftar Isi
Beberapa referensi terutama refrensi berbahasa Inggris menyebut gerak ini sebagai Projectile motion atau gerak peluru. Hal ini disebabkan semua peluru yang ditembakkan tanpa pengahlang akan membentuk lintasan parabola terbalik.
A. Konsep Gerak Parabola
Misalkan seorang anak menendang bola ke arah gawang dengan sudut tendangan θ dari tanah. Bola akan segera melesat membentuk lintasan parabola seperti pada ilustrasi di bawah ini!

Pada bola ditendeng, kaki akan memberikan impuls kepada bola sehingga menghasilkan kecepatan tertentu yakni vo. Semakin besar vo maka semakin jauh jarak bola akan melayang di udara. Analisis vektor dari persitiwa di atas terlihat pada ilustrasi bawah!

Rentetan kejadian mulai dari bergerak sebagai berikut!
- Sesaat setelah bola ditendang dengan sudut θ, maka benda akan memiliki kecepatan awal vo ke arah θ.
- Kecepatan vo ini kemudian membuat bola melesat sampai di titik Rmaks yakni titik terjauh bisa disbeut sebagai Jangkauan (Range).
- Gerak bola di udara ini sebenarnya adalah dua buah gerak yang saling berpadu yakni ke arah atas pada sumbu y dengan gerak lurus berubah beraturan dan gerak lurus beraturan pada sumbu x.
- Bola akan bergerak ke atas dengan gerak diperlambat sampai kecepatan arah y habis atau menjadi 0. Pada posisi ini, gerak bola ke arah sumbu y berbalik ke bawah dalam bentuk gerak jatuh bebas.
- Waktu yang dibutuhkan bola mencapai ymaks sama dengan waktu yang dibutuhkan benda pada saat turun.
- Rmaks di capai benda pada saat waktu benda 2 kali tymaks.
- Berdasarkan ilustrasi di atas maka variabel yang diketahui adalah vo,θ, dan g.
Dengan demikian mari analis gerak ini di masing komponen.
Gerak ke arah y
Ketinggian Maksimum
Benda akan bergerak ke arah y dengan kecepatan awal:
voy = vo sin θ
Bergerak diperlambatan dengan nilai perlambatan -g karena arah gerak melawan grafitasi. Maka ymaks dapat dihitung dengan persamaan.
v_{y_{maks}}^2=v_{oy}^2-2ghmasukkan nilai vymaks = 0, dan voy = vo sin θ maka persamaan ini menjadi
0=v_o^2 \sin^2 θ -2gy_{maks}y_{maks}=\frac{v_o^2 \sin^2 θ}{2g}Waktu Ketinggian Maksimum
Sekarang untuk waktu agar mencapai ketinggian maksimum bisa mengginakan persamaan :
v_{y_{maks}}=v_{oy}-gt_{y_{maks}}masukkan nilai vymaks = 0, dan voy = vo sin θ maka persamaan ini menjadi
0 = v_0 \sin θ -gt_{y_{maks}}t_{y_{maks}}=\frac{v_0 \sin θ}{g}Gerak ke arah x
Perhatikan nilai tymaks, ini adalah rentang waktu yang dibutuhkan agar mencapi puncak atau setengah dari parabola, dengan demikian maka untuk mencapai Rmaks akan sama dengan 2tymaks. Keran gerak ke arah sumbu x adalag GLB maka Rmaks adalah :
R_{maks}=v_{ox}2t_{y_{maks}}Masukkan semua nilai untuk 2tymaks dan vox, maka
R_{maks}=v_0\cos θ.2.\frac{v_0 \sin θ}{g}R_{maks}=\frac{v_0^2.2 \cos θ\sin θ}{g}persamaan ini bisa ditulis lebih sederhana dengan memasukkan identitas trigonometri dimana
\cos θ\sin θ =\frac{1}{2}\sin^2 θdengan demikian Rmaks adalah :
R_{maks}=\frac{v_0^2.\sin^2 θ}{g}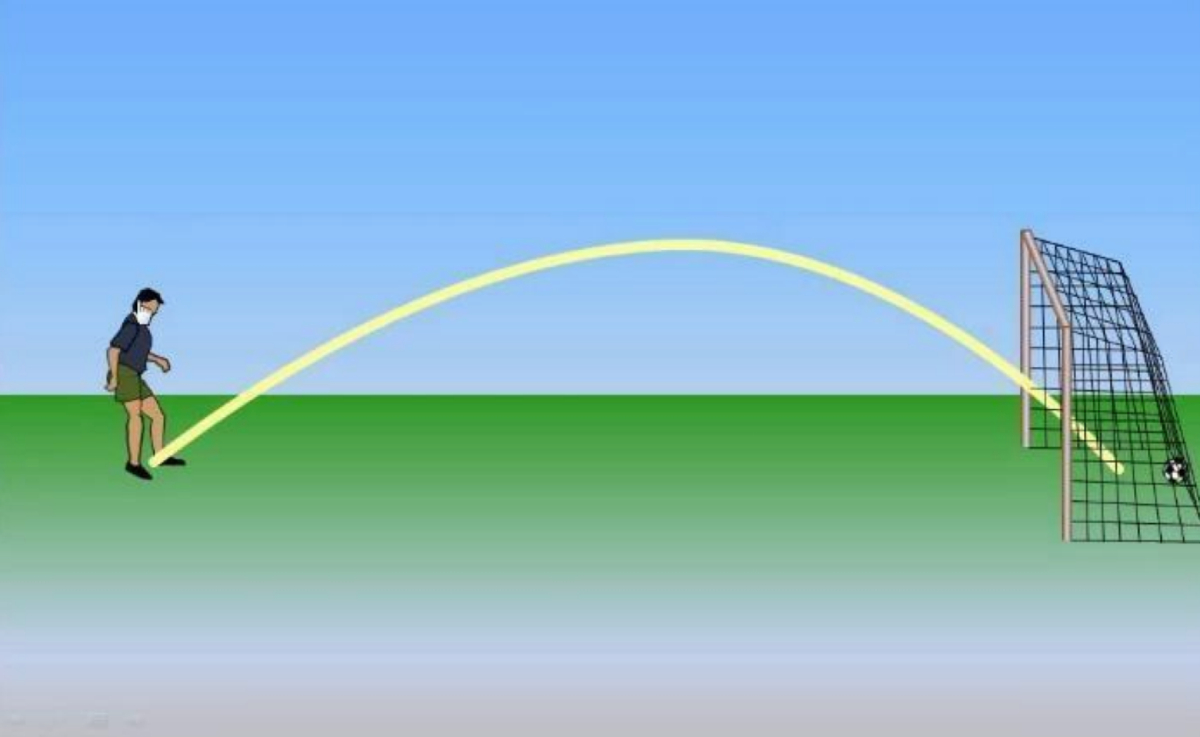
Leave a Reply
You must be logged in to post a comment.