Operasi Matematis pada Besaran Vektor

Ahmaddahlan.NET – Vektor adalah sebuah besaran yang memiliki nilai dan arah. Simbol dari besaran vektor adalah tanda panah (→) di atas huruf besaran. Misalnya pada besar kecepatan simbol v akan ditambahkan dengan simbol v vektor.

\vec v \ \ \ \ \ ..._{(1)}

Misalkan sebuah vektor berasal dari sebuah titik A (x₁,y₁) menuju titik B (x₂,y₂). Vektor ini bisa digambarkan dalam sistem koordinat cartesian. 

Vektor ini bisa diproyeksikan ke arah x dan y dimana A_x = x₂ – x₁ dan A_y = y₂ – y₁. A_x dan A_y selanjutnya dikenal sebagai komponen vektor. Komponen vektor ini selanjutnya dapat ditulis dalam bentuk matriks.

A. Jenis-Jenis Vektor

Vektor terbagi atas empat jenis yakni:

Vektor Posisi – Vektor yang ditinjau dari titik acuan (origin) 0 (0,0) sampai ke titik ujung misalnya titik A (x₁,y₁).

Vektor Nol – Vektor yang panjang dan nilai adalah 0 dan disimbolkan . Vektor ini memiliki arah namun tidak bisa ditentukan dengan jelas.

Vektor satuan – Vektor satuan adalah vektor yang nilai dan panjangnya satu satuan. Vektor satuan     adalah : .

Vektor Basis – Vektor basis adalah vektor yang saling tegak lurus satu sama lain. dalam vektor dua dimensi A_xy memiliki dua varian vektor yakni = (1 0) dan =(0 1) sedangkan untuk vektor tiga dimensi A_xyz memiliki tiga varian vektor yakni= (1 0 0) dan =(0 1 0) dan = (0 0 1). 

B. Besar dan Arah Vektor

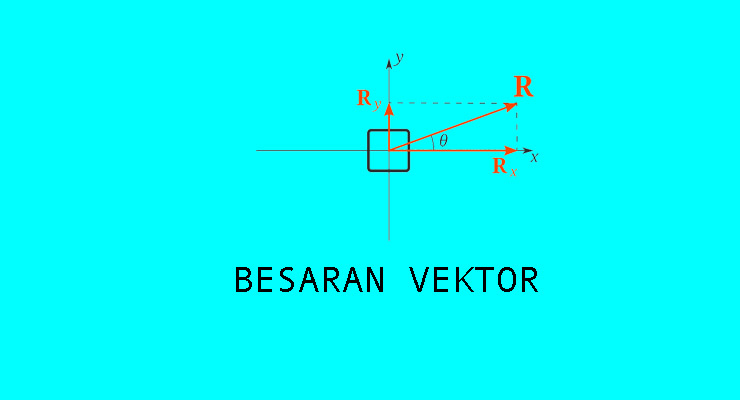
Misalnya sebuah vektor adalah vektor dua dimensi seperti pada gambar.

Panjang segmen dari vektor disebut sebagai magnitude atau besaran dinotasikan dalam bentuk dengan besar nilai resultan .

Arah dari vektor tersebut bisa dihitung sesuai dengan teorema trigonometri dimana θ = v₂/v₁. Vektor ini dapat ditulis dalam kombinasi linier dari vektor basis :

C. Operasi Vektor

Vektor adalah besaran yang dapat dioperasikan matematika sesaui dengan aturan vektor. (Comming Soon)

1. Penjumlahan Vektor

Vektor dapat mengalamai operasi matematis seperti penjumlahan. Proses penjumlahan vektor dilakukan dengan menjumlahkan komponen vektor yang seletak yang biasanya dikenal dengan Metode Poligon sedangkan tuurnan dari Metode Poligon menghasilkan Metode Jajaran Genjang.

Dua Vektor A dan Vektor B dapat mengalami operasi penjumlahan satu sama lain.

Penjumlahan antara Vektor A dan Vektor akan menghasilkan Resultan Vektor R. Nilai dari Vektor = + . Nilai Resultan Vektor adalah : 

= A_x +i