Turunan Hukum Rayleigh-Jeans Tentang Radiasi Termal

AhmadDahlan.NET – Hukum Radiasi Termal Rayleigh-Jeans adalah hukum yang menjelaskan energi yang diradiasikan oleh sebuah benda per satuan luas. Hukum ini sangat bermanfaat dalam mempelajari fenomena radiasi meskipun tidak secara sempurna memprediksi radiasi termal dari spektrum panjang gelombang.

Menurut hukum Rayleigh-Jeans, rapat energi u_ν per interval frekuensi (ν) adalah :

u_ν=\frac{8 \pi ν^2kT}{c^2}

dimana :

k : konstanta Boltzmann
T : suhu benda dalam Kelvin
c : Kecepatan Cahaya di ruang hampa.

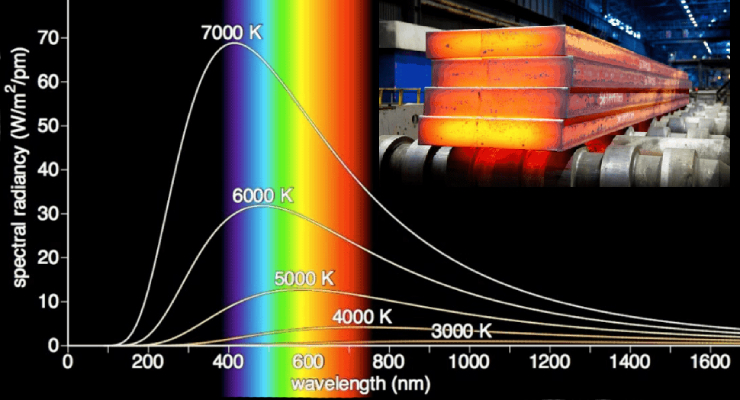
Persamaan ini fit dengan hasil pengukuran untuk radiasi dengan frekuensi rendah namun gagal untuk frekuensi tinggi. Perbedaan hasil pengukuran dan persamaan diatas dimulai dari frekuensi yang lebih tinggi dari cahaya tampak warna ungu sehingga disebut sebagai Bencana Ultraviolet.

Kesimpulan yang ditarik dari keterbatasan hukum ini menjelaskan radiasi benda mengarah pada keadaan asimtotik untuk persamaan lain tentnag radiasi benda. Hal inijuga berdampak pada nilai konstanta yangberubah-ubah pada permsaan radiasi termal Planck.

A. Penurunan Hukum Rayleigh-Jeans

Misalkan saja radiasi diapnacarkan oleh sebuah benda berbentuk kubus dengan panjang sisi L yang menjadi bidang pantul dari radiasi yang ada di dalamnya.

Gelombang berdiri terbentuk dari radiasi dengan panjang gelombang λ yang ada di dalam kubus dalah integral dari sikulus setengah gelombang yang fit dengan dimensi kubus. Dengan demikian radiasi pararel antar tepi kubus adalah :

\frac{l}{λ/2} = m

dimana m adalah bilangan bulat.

λ=\frac{2L}{m}

Di antara dua ujung akan ada dua gelombang berdiri untuk setiap polarisasi. Agar lebih sederhana, abaikan polarisasi terlebih dahulu agar memudahkan proses analisis. Karena frekuensi ν adalah c/λ, maka :

ν = \frac{cm}{2L}

Misalkan q adalah bilangan gelombang yang didefenisikan :

q= \frac{2 \pi}{\lambda}

masukkan nilai ν = c/λ, maka

q=\frac{2\pi \nu}{c}

ganti nilai ν dengan kondisi gelombang di dalam kubus maka

q=\frac{2\pi m}{2L}=\pi \frac{m}{L}

dengan demikian

q^2= \pi^2(\frac{m}{L})^2

Jika radiasi terjadi pada tiga sumbu yakni m_x, m_y, dan m_z, maka persamaan di atas bisa di tulis

q^2=\pi^2 \left [ \left ( \frac{m_x}{L} \right )^2 +\left ( \frac{m_y}{L} \right )^2+ \left ( \frac{m_z}{L} \right )^2 \right ]

Persamaan ini bisa disederhanakan dengan menggunakan frekuensi sudut yakni ω=2πν dan q = ω/c. Sehingga persamaanya menjadi :

m_x^2+m_y^2+m_z^2 = \frac{4L^2 \nu^2}{c^2}

Selanjutnya mari kita lanjutkan dengan menghitung kombinasi sebaran radiasi dalam bentuk bola untuk daerah non negatif di sumbu x,y, dan z. Ilustrasi bentuk lingkarannya sebagai berikut :

Bentuk ruang tersebut adalah seperempat bola dengan daerah di dalam R dan daerah di luar bola yakni R+dR. Volume Bola diberikan melalui persamaan :

dV = 4 \pi R^2 dR

Menurut Koordinat Bola, mak anilai R adalah

R =\sqrt{m_x^2+m_y^2+m_z^2}

maka :

R = \sqrt{\frac{4L^2 \nu^2}{c^2}} = \frac{2L \nu}{c}

karena L dan c bernilai konstan maka

dr = \frac{2L. d\nu}{c}

dengan demikian maka dV dapat ditulis :

dV = 4 \pi \frac{4L^2 \nu^2}{c^2} \frac{2L}{c}d\nu =\frac{32 \pi L^3ν 
2}{c^3} d\nu

Untuk kasus dua dimensi, ruang non-negatif berbentuk seperempat Lingkaran, pada Bola ruang ini berbentuk seperdelapan lingkaran. Dengen demikian dN untuk ruang ini hanya 1/8 dari volume bola penuh.

dN=4πν^2dν

Rata-rata energi Kinetik untuk setiap derajat kebebasan adalah :

\frac{1}{2}kT 

Dimana k adalah konstantan Blotzmann. Pada osilasi harmonik terdapat hubungan antara energi kinetik dan energi potensial sehingga rata-rata energi setia derajat bebas adalah kT. Hal ini berarti bahwa radiasi rata-ratat energi E untuk setia frekuesi adalah :

\frac{dE}{dν} =kT \left ( \frac{dN}{dν} \right ) = 4 \pi kT \left ( \frac{L^3}{c^2} \right ) ν^2

dan rapat energi rata-rata adalah, u_ν,

\frac{du_ν}{dν}=\left ( \frac{1}{L^3} \right )\left ( \frac{dE}{d\nu} \right ) = \frac{4 \pi kT\nu^2}{c^3}

Kita kembali asumsi awal dari pernurunan ini dimana tidak mempertimbangkan polarisasi gelombang dengan demikian faktor ini di kali 2 menjadi :

\frac{du_ν}{dν}= \frac{8 \pi kT\nu^2}{c^3}

Persamaan ini tepat menhitung radiasi gelombang dengan frekuensi renda sampai ke arah 0.