Ahmaddahlan.NET – Gerak pada pegas merupakan salah satu gerak yang dapat dianalisis melalui persamaan diferensial biasa orde II (PDB Orde II). Gerak ini mengikuti hukum Newton tentang gerak. Asumsinya ada dua yakni jika terjadi secara harmonis dan tidak harmonis.

Gerak Harmonis Pegas diterapkan dengan asumsi tidak ada gaya luar yang bekerja pada pegas sehingga ketika egas diberi ganguan / simpangan, pegas akan terus berayun selaman dengan periode tetap. Asumsi ke dua jika ada gaya eksternal yang bekerja pada pegas yang nilainya kecil, maka pegas akan akan berhenti pada satu waktu tersebut. Gerak pegas ini disebut Teredam lembut atau Dumped Oscillation.

Pada sebuah pegas yang digantung beban akan terdapat empat kemungkinan gaya masing adalah :

1. Gaya berat w = mg
2. Gaya pemulih F_k = -k (y+Δy)
3. Gaya Peredam pada pegas F_D = -Dv_y
4. Gaya Eksternal F_e

Misalkan pegas diberi ganguan sehingga pegas mulai bergerak maka berlaku hukum Newton II tentang gerak

ΣF = ma

Persamaan ini kemudian di subtitusi dengan semua gaya yang bekerja pada pegas sehingga menjadi

W_b+F_k+F_D+Fe = ma

mg - ky - kΔy -Dv_y + F_e = ma

Karena mg = -ky dan v_y adalah turunan pertama perubahan posisi terhadap waktu dy/dt maka persamaan ini dapat dituls lebih sederhana.

-kΔy -D\frac{dy}{dt}+ F_e = m\frac{d^2y}{dt^2}

Jika Δy adalah besara simpangan maka bisa dianggap sebagai y, dengan demikian Bentuk umum persamaan diferensial biasa Orde II untuk Gerak harmonik pada pegas adalah :

m\frac{d^2y}{dt^2} +D\frac{dy}{dt}+ky =F_e

A. Analisis Matematis Gerak Harmonis Pegas

Pada gerak pegas yang berosilasi harmonik sederhana ada dua asumsi yang dimasukkan yang tidak ada gaya peredam dan gaya eksternal yang bekerja sehingga persamaan gerak dapat ditulis :

m\frac{d^2y}{dt^2} +ky =0

bagi kedua ruas dengan m

\frac{d^2y}{dt^2} +\frac{k}{m}y =0

Pada saat pegas berada pada percepatan maksimum nilai k/m = ω², sehingga

\frac{d^2}{dt^2} y+ω^2y =0

(\frac{d^2}{dt^2} +ω^2)y =0

Misalkan :

\frac{d^2}{dt^2} = r^2

maka bisa disimpulkan

r^2 + ω^2 = 0

Persamaan ini r²+ω²=0 memiliki akar-akar yang homogen seperti pada Solusi Umum PBD Orde II yakni r_1,2 = ±iω₀ dengan solusi :

y_{(t)}=c_1 \cosω_0t+c_2\sinω_0t

Untuk menentukan nilai konstanra c₁ dan c₂, kita lakukan sedikit trik dengan mengalikan ke dua ruas dengan :

\frac{\sqrt{c_1^2+c_2^2}}{\sqrt{c_1^2+c_2^2}}=1

Sehingga persamaan dapat ditulis dengan :

y_{(t)}=\sqrt{c_1^2+c_2^2}(\frac{c_1}{\sqrt{c_1^2+c_2^2}} \cosω_0t+\frac{c_2}{\sqrt{c_1^2+c_2^2}}\sinω_0t)

Misalkan R²=C₁²+C₂², diambil dari sebuah segitiga siku-siku, maka

\cosθ=\frac{c_1}{\sqrt{c_1^2+c_2^2}} 

dan

\sin θ= \frac{c_2}{\sqrt{c_1^2+c_2^2}}

Sehingga solusi y_(t) dapat ditulis :

y_{(t)}=R (\sinθ\cos ω_0t+\cosθ\sin ω_0t)

Bisa disederhanakan dengan indetintas Trigonometri yakni

y_{(t)}=R \cos (ω_0t±θ)

Dimana
y_(t)= simpangan gelombang
R = Amplitudo
θ = bilangan gelombang
ω₀ = frekuensi sudut dimana ω₀²=k/m

B. Analisis Matematis Gerak Pegas Teredam Lembut

Pada kasus dunia nyata misalnya sebauh pegas yang dipasang pada sebuah motor. Pegas akan mendapatkan gaya peredam dari pegas agar getaran berhenti.

m\frac{d^2y}{dt^2} +D\frac{dy}{dt}+ky =F_e

Pada kasus Pegas teredam Lembut maka F_e adalah nol, sehingga peredam hanya berasal dari gaya peredam pegas.

m\frac{d^2y}{dt^2} +D\frac{dy}{dt}+ky =0

Kita gunakan pemisalan r = d/dt, sehingga persamaan ini dapat ditulis

(m.r^2+D.r+k)y=0

dengan demikian :

m.r^2+D.r+k=0

Pada kasus terdeam lembut Diskiriman berlaku D² – 4mk < 0 sehingga akar-akar dapat dinyatakan dalam bilangan real dengan bentuk :

r_{1,2}=\frac{-b±i\sqrt{4mk-D^2}}{2m}=\frac{-b}{2m}±\frac{i\sqrt{4mk-D^2}}{2m}

suku pertama adalah α dan β. Bentuk solusi dari dari persamaan ini adalah :

y_{(t)}=c_1e^{α +iβt}+c_2e^{α -iβt}

masukkan nilai α dan β, sehingga solusinya gerak terdemannya menjadi

y_{(t)}=Re^{\frac{-d}{2m}t}\cosβt-θ

Dimana R adalah Simpangan maksimum awal atau y₀

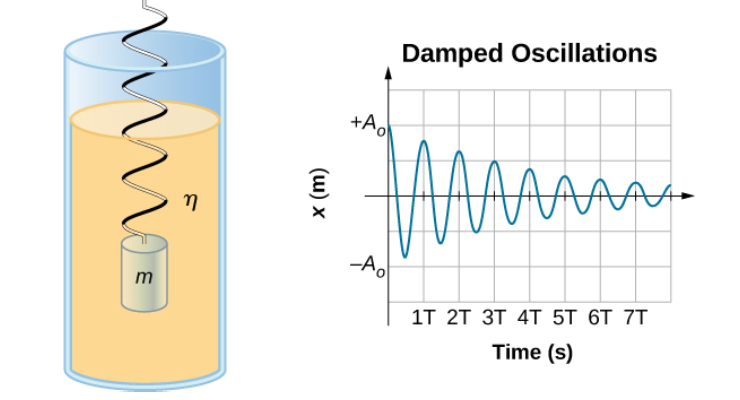
Bentuk Getarannya seperti berikut :