Lingkaran merupakan bidang datar yang dimensinya ditentukan oleh jari-jari (r). Seluruh nilai seperti panjang busur dan luas juring ditentukan oleh nilai r dan sudut pusatnya.
Daftar Isi
Sudut Pusat, Panjang Busur dan Luas Juring
Misalkan sebauh lingkaran ditunjukkan pada gambar di bawah ini.

a. Busur
Busur adalah garis lengkung yang merupakan bagian dari keliling lingkaran, misalnya pada gambar diatas busur AB dan CD. Panjang busur dapat dihitung dengan membandingkan besar sudut pusat dan keliling lingkaran.
Panjang Busur AB ditentukan oleh besar sudut pusat merah atau ∠AOB = x°, demikian pulan Busur CD yang ditentukan ∠COD = y°.
Rumus Panjang Busur
AB=2\pi r\frac{∠AOB}{360^o}CD=2\pi r\frac{∠COD}{360^o}b. Juring
Juring adalah adalah luas daerah yang besarnya ditentukan oleh sudut pusat. Pada gambar di atas terdapat dua buah Juring yakni Juring Merah AOB dan Juring Biru yakni COD.
Rumus Luas Juring
A_{AB}=\pi r^2\frac{∠AOB}{360^o}A_{CD}=\pi r^2\frac{∠COD}{360^o}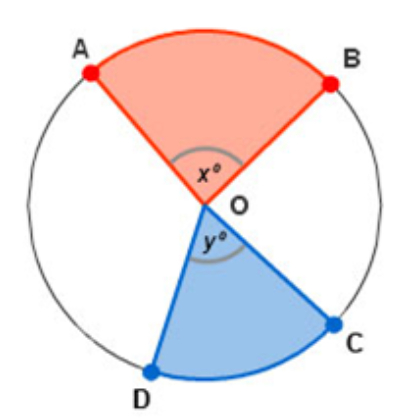
Leave a Reply
You must be logged in to post a comment.