AhmadDahlan.NET – Beberapa keadaaan pada termodinamika dikaji melalui bantuan pemodelan matematis. Tujuannya untuk memudahkan proses separasi peran dari masing-masing variabel bebas. terhadap nilai dari variable terikat.
Daftar Isi
A. Teorema Matematis
Misalkan saja pada objek termodinamis terdiri dari tiga koordinat yang saling berhubungan x, y dan z, maka hubungan ini dapat ditulis dalam bentuk :
\[f_{(x,y,z)}= 0\]dimana
x adalah fungsi dari y dan z, maka :
\[dx=\left ( \frac{δx}{δy} \right )_z dy+\left (\frac{δx}{δz} \right )_y dz\]y adalah fungsi dari x dan z, maka :
\[y=\left ( \frac{δy}{δx} \right )_z dx+\left (\frac{δy}{δz} \right )_xdz\]Jika persamaan satu dimasukkan persamaan dy ke persamaan dx maka hasilnya sebagai berikut :
\[dx=\left ( \frac{δx}{δy} \right ) _z \left [ \left (\frac{δy}{δx} \right )_z dx + \left (\frac{δy}{δz} \right )_x dz\right ]+\left ( \frac{δx}{δz} \right ) _y dz\] \[dx=\left ( \frac{δx}{δy} \right ) _z\left (\frac{δy}{δx} \right )_z dx \ + \left[ \left ( \frac{δx}{δy} \right ) _z\left (\frac{δy}{δz} \right )_x +\left ( \frac{δx}{δz} \right ) _y \right]dz\]Misalkan dari tiga koordinat hanya terdapat dua yang bebas yakni (x,z), jika dz=0 dan dx ≠ 0, maka :
\[\left ( \frac{δx}{δy} \right ) _z\left (\frac{δy}{δx} \right )_z = 1\]jika dx = 0 dan dz ≠ 0, maka
\[\left ( \frac{δx}{δy} \right ) _z\left (\frac{δy}{δz} \right )_x +\left ( \frac{δx}{δz} \right ) _y = 0\] \[\left ( \frac{δx}{δy} \right ) _z\left (\frac{δy}{δz} \right )_x =-\left ( \frac{δx}{δz} \right ) _y\]dengan demikian
\[\left ( \frac{δx}{δy} \right ) _z\left (\frac{δy}{δz} \right )_x \left ( \frac{δz}{δx} \right ) _y =-1\]B. Contoh Aplikasi
Setiap infinitesimel dalam koordinat termodinamika (P, V, T). Hubungan antara variabel dapat di hitung dengan nilai yang berubah terhadap dua variable lainnya.
Misalnya variabel V adalah fungsi dari (T,P) maka nilai V dapat ditentukan dengan persamaan diferensial parsial yakni :
\[dV = \left ( \frac{δV}{δT}\right )_p dT \ + \left ( \frac{δV}{δP}\right )_TdP\]Kuantitas pemuaian volume rata-rata didefenisikan sebagai :
\[muai \ volume \ rata-rata = \frac{perubahan \ volume /satuan \ volume}{perubahan \ temperatur}\]Pada kondisi isobar.
Jika perubahan temperature sangat kecil, maka perubahan volume juga akan sangat kecil, maka Koefisien pemuaian (β) dirumuskan :
\[β=\frac{1}{V} \left( \frac{δV}{δT}\right)_P\]Secara matematis β adalah fungsi dari (T,P) hanya saja dalam percobaan banyak zat yang memiliki nilai β yang tidak sensitif terhadapat tekanan (dP) dan hanya sedikit berubah terhadap perubahan suhu (dT).
Dampak dari perubahan tekannan pada keadada isotermik dinyatakan dalam κ (baca kappa) yang disebut ketermampatan isotermik, secara matematis dinyatakan sebagai berikut:
\[κ=-\frac{1}{V} \left( \frac{δV}{δP}\right)_T\]Berdasarkan teorema matematika maka persamaan Hidrostatik diperoleh :
\[\left ( \frac{δP}{δV} \right ) _T\left (\frac{δV}{δT} \right )_P =-\left ( \frac{δP}{δT} \right ) _V\]atau
\[\frac{\left (\frac{δV}{δT} \right )_P}{\left ( \frac{δV}{δP} \right ) _T}=-\left ( \frac{δP}{δT} \right ) _V\]masukkan dinilai persamaan β dan κ, sehingga hasilnya :
\[\left ( \frac{δP}{δT} \right ) _V=\frac{β}{κ}\]Pada kondisi Isobarik, maka bentuk diferensial parsialnya adalah :
\[dP = \left ( \frac{δP}{δT}\right )_v dT \ + \left ( \frac{δP}{δV}\right )_T dV\]maka dP :
\[dP = \frac{β}{κ}dT-\frac{1}{κV}dV\]Pada kondoso Isohorik dimana dV = 0, maka
\[\int^2_1 dP = \frac{β}{κ} \int^2_1 dT\] \[P_2-P_1 =\frac{β}{κ}(T_2-T_1)\]Tugas :
Buktikan bahwa :
\[β=\frac{1}{T}\]dan
\[κ=\frac{1}{P}\]Pada gas ideal dengan persamaan PV = RT !!!
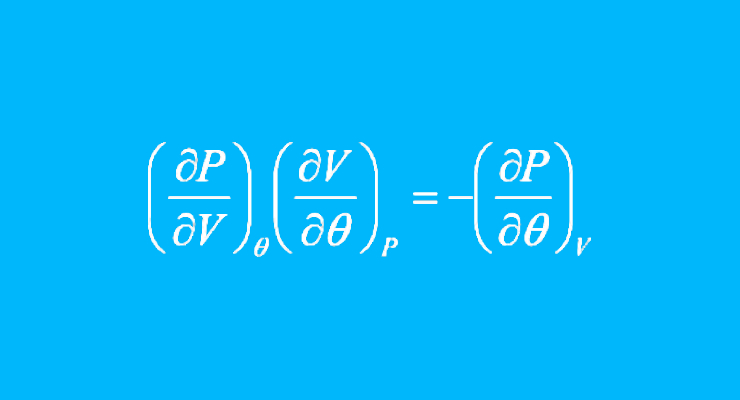
Leave a Reply
You must be logged in to post a comment.